当某温度下，驱动电压为V，负载P下的桥臂电阻变化为ΔR时，相应的理想差分输出：

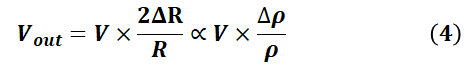
我们往往还会定义一个参数叫灵敏度S，单位为（mV/V/kPa），如下描述。

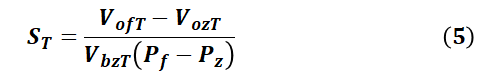
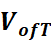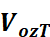上式中，是指同一温度T下， 和 分别为满量程输出和0点输出差分电压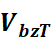； 为0负载时的电桥驱动电压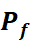； 和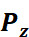 分别指满量程压强和0负载对应的压强。不同温度下 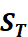还不一样，所以有TCS：

灵敏度温度系数TCS，是指在高低温度h，c两处的灵敏度Sh 、Sc 相对于参考温度r处的灵敏度Sr 在测量温度范围内每摄氏度的变化量。

其实以上各参数计算时，都默认是线性变化量。工程应用上，如果一定范围内精度足够，即使非线性我们也会将其化为线性再处理，反之，如果要进一步提高数据精度，则要对各参数进行更高阶的设定。

如何降低温度对输出的影响

必要说明的是，在硅压阻压力产品参数中，TCR和TCS的正负，以及大小，都是在设计中有选择实现的。根据上一个段落中对TCR和TCS的线性化定义描述，我们可以先做以下的简单设定：

桥臂阻值用TCR表示为：

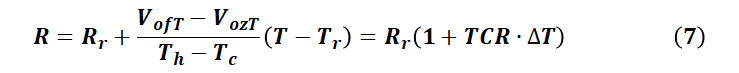
类似方式，灵敏度用TCS可以表示为：

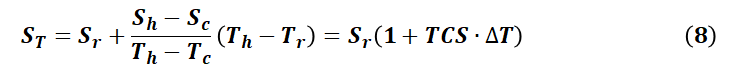
由于实际使用中，对于电桥的驱动方式有两类，一类是恒流，另一类是恒压（我们把比率方式归入这类型）。关于比率方式，大家可以参考一下有关文档，以及我们之前发的应用文档，包括：

• 《NPC-1210压力传感器在板增益电阻的特性分析及信号放大注意事项》

• 《ADC参考电压的选择 — 比率还是绝对》

• 恒流激励下的温度补偿

在恒流激励I的设定下，设想电桥输入阻抗Ri 未变，而温度T上升时，从式（4）和（5）中可以这样大致认为，即使相应的激励电压V= I×Ri 和负载压强P不变，在TCS<0的情况下，如果T增加∆T ，式（8）中的灵敏度ST 则减小，所以，对应的差分电压输出有：

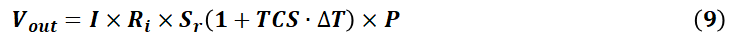
如果式（9）中只有温度变化∆T ，由于TCS<0，所以输出信号Vout 会减小。然而，由于TCR>0，如果各项参数都符合对惠斯通电桥对称的设定，此时可以近似得到如下式（10），电桥的输入阻抗Ri 此时将增大，由此驱动电桥的电压将增大。

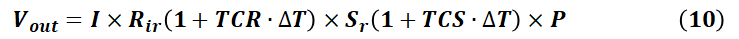
式（10）中即有增大的变量，又有减小的成分。所以，某种程度上，TCR的增大可以对TCS的减小有所补偿。但是可以肯定的是，一个包含∆T 二次项的方程，最多也就有2个解或者2个点刚好抵消。这两者是不会完全抵消的。